CONGRUENCIA DE TRIÁNGULOS EJERCICIOS RESUELTOS PDF
PROBLEMAS RESUELTOS
PREGUNTA 1 :
En la figura, PQ=AP+QB. Si AM =5√2m, BN=5m y MN =5√3m, ¿cuál es la medida del ángulo determinado por las prolongaciones de los segmentos AM y de BN?
A) 60°
B) 53°
C) 75°
D) 90°
RESOLUCIÓN :
Rpta. : "D"
OBJETIVOS DE APRENDIZAJE
• Identificar los triángulos congruentes a partir de su relación entre lados y ángulos, (casos de congruencia).
• Relacionar correctamente los lados de igual longitud y ángulos de igual medida en dos triángulos congruentes.
• Aplicar la congruencia en la resolución de los ejercicios.
CUESTIONES PREVIAS
– En la geometría euclidiana, la congruencia es equivalente a igualdad.
– Dos segmentos serán congruentes cuando tengan igual longitud.
– Dos ángulos serán congruentes cuando tengan igual medida.
– Dos triángulos serán congruentes cuando los lados y ángulos del primero sean de igual medida que los lados y ángulos del segundo respectivamente.
CONGRUENCIA DE TRIÁNGULOS
Dos triángulos serán congruentes cuando los lados y ángulos del primero sean de igual medida que los lados y ángulos del segundo respectivamente.
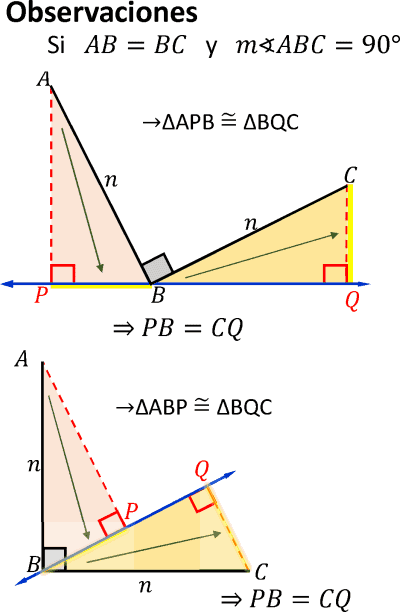
OBSERVACIONES EN LOS TRIÁNGULOS CONGRUENTES
• A lados de igual longitud se les oponen ángulos de igual medida.
• A ángulos de igual medida se les oponen lados de igual longitud.
LADO ÁNGULO LADO (LAL)
Dos triángulos serán congruentes cuando dos lados del primero sean de igual longitud que dos lados del segundo y el ángulo entre ellos de igual medida.
ÁNGULO LADO ÁNGULO (ALA)
Dos triángulos serán congruentes cuando dos ángulos del primero sean de igual medida que dos ángulos del segundo y el lado entre ellos de igual longitud.
LADO LADO LADO (LLL)
Dos triángulos serán congruentes cuando Los lados del primero sean de igual longitud que los lados del segundo.
NOTAS
• Tres casos que no requieren de los tres lados y los tres ángulos para que sean congruentes.
• En estos casos tienen que haber tres elementos en uno que sean de igual medida que tres elementos del otro triángulo.
• En esos tres casos tienen que haber un lado igual al menos.
TRIÁNGULOS RECTÁNGULOS CONGRUENTES
Dos triángulos rectángulos serán congruentes cuando:
– Un cateto del primero sea de igual longitud que un cateto del segundo y las hipotenusas de ambos de igual longitud.
– Una hipotenusa del primero sea de igual longitud que la hipotenusa del segundo y tengan un ángulo agudo en común.