RAZONES TRIGONOMÉTRICAS DE ÁNGULOS AGUDOS EJERCICIOS RESUELTOS PDF
SENO , COSENO , TANGENTE , COTANGENTE , SECANTE Y COSECANTE DE UN ÁNGULO ÁGUDO - PROPIEDADES
Desde épocas antiguas, el cálculo de distancias inaccesibles ha sido una necesidad para poder desarrollar la construcción de templos, palacios, canales de irrigación, etc., así como para poder explicar diversos fenómenos a partir de los valores encontrados.
Ello ha motivado la creación de ciertos valores constantes que se han obtenido por la comparación entre longitudes, estos valores son llamamos razones trigonométricas.
En la ingeniería y la ciencia, en general, el uso de las razones trigonométricas ha permitido determinar no solo valores, como la distancia entre astros (la Tierra, el Sol y la Luna), el radio de la Tierra y la altura de una montaña, sino también ha permitido hacer grandes construcciones, como las pirámides, y entender muchos fenómenos, como las ondas sonoras, la corriente y los fenómenos periódicos.
TRIÁNGULO RECTÁNGULO
Se llama triángulo rectángulo al triángulo donde uno de sus ángulos es recto (90º), además recuerde que el lado opuesto al ángulo recto se llama hipotenusa y los dos lados restantes catetos.
RAZÓN TRIGONOMÉTRICA
Son aquellos números que resultan de dividir la longitud de los lados de un triángulo rectángulo.
TEOREMA DE PITÁGORAS
“La suma de cuadrados de los catetos es igual al cuadrado de la hipotenusa”
CÁLCULO DE LAS RAZONES TRIGONOMÉTRICAS
El valor de las razones trigonométricas de ángulos agudos, se determinan en un triángulo rectángulo, estableciendo la división entre las longitudes de sus lados tomados de dos en dos y con respecto a uno de sus ángulos agudos.
APLICACIONES DE LAS RAZONES TRIGONOMÉTRICAS
Las razones trigonométricas son útiles para el cálculo de distancias , en carreras como Ing. Civil , Ing. Minas ,Ing. Ambiental.
Es común en ellas utilizar conocimientos de calculo de distancias con precisión sobre terrenos o construcciones . Para dichos cálculos se necesita conocer medidas angulares que se obtienen con un instrumento llamado Teodolito.
El teodolito es un instrumento de medición mecánico óptico universal que sirve para medir ángulos verticales y horizontales, ámbito en el cual tiene una precisión elevada. Con otras herramientas auxiliares puede medir distancias y desniveles.
SENO
En un triángulo rectángulo se define como seno de un ángulo agudo al valor obtenido al dividir la longitud del cateto opuesto al ángulo entre la longitud de la hipotenusa.
COSENO
Se define como coseno de un ángulo agudo al valor obtenido al dividir la longitud del cateto contiguo al ángulo entre la longitud de la hipotenusa.
TANGENTE
Se define como tangente de un ángulo agudo de un triángulo rectángulo al valor del cociente obtenido al dividir la longitud del cateto opuesto entre la longitud del cateto contiguo.
RAZÓN
Es el resultado de comparar dos cantidades, esta comparación se expresa mediante el cociente de ellas.
OPERADOR TRIGONOMÉTRICO
Son aquellos símbolos matemáticos que se aplican a los ángulos.
RAZÓN TRIGONOMÉTRICA
Es el resultado de aplicar un operador trigonométrico a un ángulo.
EJERCICIO 1 :
Calcule los valores de las seis razones trigonométricas del menor ángulo “θ”, en un triángulo rectángulo, cuyos catetos miden 5 y 12 unidades.
EJERCICIO 2 :
En un triángulo rectángulo, los lados mayores miden 13 cm y 12 cm. Calcular el coseno del mayor ángulo agudo.
EJERCICIO 3 :
En un triángulo rectángulo, el cateto opuesto de uno de sus ángulos agudos es la mitad de la hipotenusa. Calcula el seno de dicho ángulo.
EJERCICIO 4 :
Si tanθ = 0,5 (θ: agudo)
Calcular: cscθ y secθ
EJERCICIO 5 :
El perímetro de un triángulo rectángulo es 338 m y la tangente de uno de los ángulos agudos es 2,4. ¿Cuánto mide el cateto menor?
EJERCICIO 6 :
El perímetro de un triángulo rectángulo es 36 u, además el seno de uno de sus ángulos agudos es 0,6. Calcule la longitud de la hipotenusa.
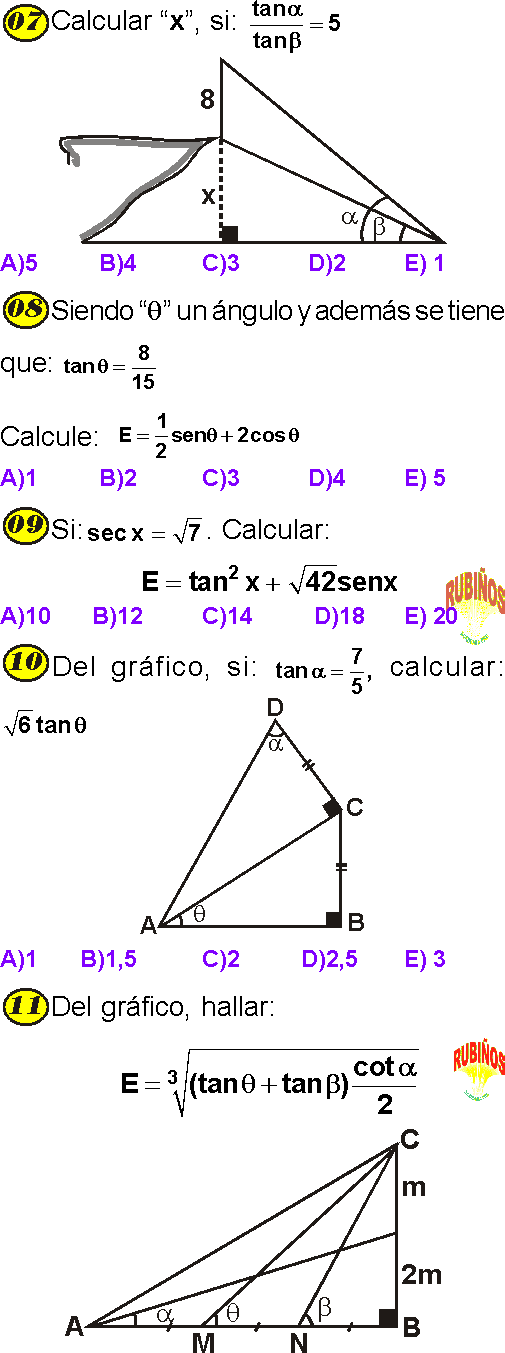
EJERCICIO 7 :
El perímetro de un triángulo rectángulo es 180 m. Si se sabe que la tangente de uno de sus ángulos agudos es 2,4. Calcular su hipotenusa .
EJERCICIO 8 :
Indica la verdad (V) o falsedad (F) de las siguientes proposiciones:
A) La cosecante de todo ángulo agudo es mayor que su coseno ...( )
B) El coseno de un ángulo puede ser igual a 3/2 ...( )
C) Para determinar el valor de las seis razones trigonométricas de un ángulo agudo es suficiente conocer el valor de solo una de ellas ...( )
D) El seno de un ángulo agudo puede medir 0,5 m ...( )
E) Si los lados de un triángulo rectángulo se duplican; entonces el seno de sus ángulos agudos también se duplica ...( )
EJERCICIO 9 :
En un triángulo rectángulo, los lados menores miden 2 y 3 cm. Si el mayor ángulo agudo es α, calcula sen²α
EJERCICIO 10 :
En un triángulo rectángulo, los lados menores miden 2 y √3 cm. Calcula el coseno del menor ángulo agudo del triángulo.
PROBLEMAS RESUELTOS
PREGUNTA 1 :
PREGUNTA 2 :
En un triángulo rectángulo que tiene un ángulo agudo “α” se cumple tgα=5senα/3.
Halle senα+cosα.
A) 6/5
B) 7/5
C) 1
D) 3
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 3 :
Del gráfico mostrado, hallar tgθ, si tgα=5/8
A) 5/4
B) 5/2
C) 3/2
D) 5/3
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 6 :
SEGUNDA GUIA
EJERCICIO 1 :
Calcula α
Si: cosα.sec7°=1
A) 1°
B) 3°
C) 5°
D) 7°
E) 14º
EJERCICIO 2 :
Calcula θ
Si : senθ.csc18°=1
A) 12°
B) 14°
C) 16°
D) 18°
E) 20º
EJERCICIO 3 :
Calcula 2θ
Si: senθ.csc(40°–θ)=1
A) 10°
B) 20°
C) 30°
D) 40°
E) 5º
EJERCICIO 4 :
Calcula ψ
Si: tg25.ctg5ψ=1
A) 20°
B) 25°
C) 30°
D) 35°
E) 5º
EJERCICIO 5 :
Calcula 4β
Si: cos2β.sec(β+10°)=1
A) 10°
B) 20°
C) 30°
D) 40°
E) 4º
EJERCICIO 6 :
Si: tg2β=ctg3β
Calcular β
A) 18°
B) 36°
C) 54°
D) 72°
E) 20º
EJERCICIO 7 :
Si: senθ=cos(θ – 2°)
Calcular θ
A) 42°
B) 44°
C) 46°
D) 48°
E) 50º
EJERCICIO 8 :
Si: sen3φ – cos15°=0
Calcula φ
A) 20°
B) 25°
C) 30°
D) 35°
E) 40º
EJERCICIO 9 :
Si: sec4ψ=cscψ
Calcular 2ψ
A) 18°
B) 36°
C) 54°
D) 72°
E) 45º
EJERCICIO 10 :
Si: tg(φ+10°)=ctg(φ+20°)
Calcula φ+10
A) 10°
B) 20°
C) 30°
D) 40°
E) 50º
EJERCICIO 11 :
Calcule:
10(sen37°+cos37º)
A) 1
B) 3
C) 5
D) 7
E) 9
EJERCICIO 12 :
Calcule:
10(cos53°+sen53°)
A) 1
B) 3
C) 5
D) 7
E) 9
EJERCICIO 13 :
Calcule:
csc53°+ctg53°
A) 2
B) 4
C) 6
D) 8
E) 10
EJERCICIO 14 :
Calcule:
csc37°+ctg53°
A) 1
B) 3
C) 5
D) 7
E) 9
EJERCICIO 15 :
Calcule:
sec37°+ctg53°
A) 2
B) 4
C) 6
D) 8
E) 12
EJERCICIO 16 :
Calcule x:
xtg45°=sen45°sec45°
A) 1
B) 2
C) 3
D) 4
E) 5
EJERCICIO 17 :
Calcular M + N Si:
M = 4cos²45°
N = 8csc²45°
A) 16
B) 18
C) 20
D) 17
E) 19
EJERCICIO 18 :
Calcule:
3sen30° – 5cos60°
A) 1
B) –1
C) 0
D) –3/2
EJERCICIO 19 :
Calcule :
sec60° – 1
A) 2
B) 3
C) 1
D) 0
EJERCICIO 20 :
Calcule
cos60°+sen30°
A) 1/2
B) –1/2
C) 1
D) 0
EJERCICIO 21 :
Calcule x en:
xtg60° = 2ctg30°–√3
A) 0
B) 1
C) –1
D) 2 5
EJERCICIO 22 :
Calcule :
sec30°cos60°
A) –2
B) –1
C) 4/3
D) 2
PROBLEMAS PROPUESTOS
PREGUNTA 1 :
En triangulo rectángulo la tangente de uno de los ángulos agudos es el triple de la tangente de su complemento; calcular el coseno del mayor ángulo agudo.
a) 1/2
b) 1/3
c) 1/4
d) 1/5
e) 1/6
Rpta. : "A"
PREGUNTA 2 :
En un triangulo rectángulo de perímetro 60 m, calcular su área, si el coseno de uno de los ángulos agudos es 0,8.
a) 120 m²
b) 130 m²
c) 140 m²
d) 150 m²
e) 160 m²
Rpta. : "D"
PREGUNTA 3 :
Calcular el perímetro de un triángulo rectángulo, cuya área es 7,5 cm², si el valor de la tangente trigonométrica de uno de sus ángulo agudos es 5/12.
a) 12 cm
b) 13 cm
c) 15 cm
d) 24 cm
e) 30cm
Rpta. : "C"
PREGUNTA 4 :
La altura desigual de un triángulo isósceles mide 15 cm; siendo su perímetro 50 cm, calcular el coseno de uno de sus ángulos iguales.
a) 15/17
b) 17/15
c) 17/8
d) 8/17
e) 8/15
Rpta. : "D"
PREGUNTA 5 :
El perímetro de un triángulo rectángulo es 120 m y el valor del seno de uno de sus ángulos agudos es 12/13 . Calcule la longitud del cateto mayor.
A) 48 m
B) 20 m
C) 52 m
D) 90 m
Rpta. : "A"
PREGUNTA 6 :
En un triángulo rectángulo T la diferencia entre las medidas de sus catetos es 1 cm y la hipotenusa excede en 8 cm a la medida de su cateto mayor.
29(senψ + cosψ), siendo ψ el ángulo menor de T.
A) 41
B) 29
C) 40
D) 42
E) 39
Rpta. : "A"
PREGUNTA 7 :
En un triángulo T (de vértices A, B y C) se cumple que
17senA – 15 = 0
5senC – 3 = 0
Si AC = 28 cm, ¿en cuánto excede la longitud del lado mayor de T a la del menor?
A) 11 cm
B) 10 cm
C) 3 cm
D) 5 cm
E) 8 cm
Rpta. : "A"
PREGUNTA 8 :
En un triángulo rectángulo uno de los catetos mide 8 u y el otro dos unidades menos que la hipotenusa. Hallar el seno del menor ángulo.
A) 8/15
B) 7/9
C) 5/7
D) 8/17
E) 8/19
Rpta. : "D"
PREGUNTA 9 :
Eloy tiene un huerto en forma de un triángulo rectángulo y quiere cercarlo con una malla. Aficionado a las matemáticas, decide nombrar con las letras A, B y C los vértices del huerto, siendo el triángulo recto en B.
Si tanA =12/5
a+ c = 34 m
Determine la cantidad de malla que tiene que comprar.
A) 60 m
B) 70 m
C) 80 m
D) 90 m
Rpta. : "A"
PREGUNTA 10 :
Dado un triángulo ABC, la expresión:
K = a(1+Cos B) + b(1+Cos A)
representa:
a) Área
b) Doble del área
c) Perímetro
d) Doble del perímetro
e) Semiperimetro
Rpta. : "C"
APRENDIZAJES ESPERADOS
• Reconocer el cateto opuesto, adyacente e hipotenusa en un triángulo rectángulo.
• Definir las razones trigonométricas seno, coseno y tangente.
• Aplicar las razones trigonométricas de ángulos agudos.
• Definir las razones trigonométricas cotangente, secante y cosecante.
• Aplicar las razones trigonométricas en diversos problemas.
OBJETIVOS FINALES :
• Reconocer los lados del triángulo rectángulo
• Conocer el teorema de Pitágoras
• Aprender a utilizar el Teorema de Pitágoras para el cálculo de las medidas de las longitudes de la hipotenusa o un cateto.
• Calcular las razones trigonométricas seno y coseno conociendo las medidas de las longitudes de dos o más lados de un triángulo rectángulo.
• Aprender la diferencia entre las razones trigonométricas seno y coseno.
• Realizar operaciones matemáticas con las razones trigonométricas (R.T.)
• Reconocer las razones trigonométricas tangente y cotangente.
• Aplicar estas razones para determinar distancias en un triángulo rectángulo
• Reconocer las razones trigonométricas secante y cosecante.
• Calcular los lados de un triángulo rectángulo usando correctamente las razones trigonométricas sec y sec.
• Analizar y comprender las razones trigonométricas recíprocas.
• Deducir las razones trigonométricas recíprocas.
• Reconocer las razones trigonométricas complementarias.
• Relacionar las medidas de los ángulos en las razones trigonométricas complementarias (90º).
• Resolver problemas aplicando los criterios de las razones trigonométricas complementarias
• Reconocer la proporcionalidad de los lados del triángulo rectángulo 37º - 53º.
• Calcular las razones trigonométricas de los ángulos 37º - 53º.
• Aplicar las razones trigonométricas en la resolución de problemas.
• Aplicar las razones trigonométricas 37º - 53º en el cálculo de los lados de un triángulo.
• Calcular distancias y alturas utilizando razones trigonométricas de 37º - 53º.
• Reconocer la proporcionalidad de los lados de un triángulo rectángulo de 45º.
• Calcular las razones trigonométricas del ángulo de 45º
• Aplicar las razones trigonométricas en el cálculo de expresiones
• Reconocer los triángulos notables por la medida de sus ángulos agudos
• Reconocer los triángulos notables por la proporcionalidad de sus lados
• Calcula los lados de un triángulo notable usando razones trigonométricas
• Determina las razones trigonométricas de los ángulos (30º y 60º)
• Reconocer las diferentes aplicaciones de los triángulos notables.
• Identificar el ángulo agudo y formar el triángulo rectángulo cuando observamos objetos por debajo o por arriba de nuestros ojos.
• Aplicar casos de la vida práctica, los conceptos de razones trigonométricas de triángulos notables.